Category: Entries

Taking as base the raw image dataset, without any additional information except for the pixels that make up their digital representations, each image was analyzed with a Convolutional Neural Network (CNN). For computers, images are nothing more than giant tables of numbers. Thus, a grayscale image of 100 × 100 pixels (100 high by 100 wide) can be seen as a table with 100 rows and 100 columns in which each cell contains a value that encodes the amount of white it contains. Black usually corresponds to the lowest value, 0; while the highest value is reserved for white. This higher value is arbitrary and depends on the desired color depth. It is usually common to encode up to 256 levels, requiring 1 byte to store each pixel (1 byte = 2 ^ 8 = 256). If instead of a grayscale image we have color images, each color is broken down into its components according to a color model. The RGB model, for example, decomposes each color additively into the amount of red (Red), green (Green), and blue (Blue), thus needing 3 values ​​each between 0 and 256 to encode a color. This translates into storing a 3-dimensional point in each of those cells, or having 3 tables for each color component.

These tables or matrices are the inputs of the CNN. (Artificial) neural networks are machine learning systems loosely inspired by the biological neural networks present in the brains of animals. These systems “learn” to perform operations from examples, generally without being programmed with specific rules for each task. Internally, such a network is based on a set of connected units or nodes, called artificial neurons, that model the neurons of a biological brain. Each connection, like synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron that receives a signal processes it and can signal neurons connected to it. The connections between neurons are weighted and the neurons are usually arranged in layers that connect sequentially (although this configuration allows for variations). The last layer is usually the output layer and is adjusted, in the case of supervised learning, to the number of cases to predict: cat vs. dog, person vs. animal, or multiple classes if necessary. Initially, the weights of the neurons are randomly distributed. When an input is processed, it passes through all the neurons according to how each one is activated, and upon reaching the output, the result is compared with the expected result -a difference known as loss-, adjusting the weights of the connections so that in the next iteration the output is more like expected; that is, the loss is minimized. With the sufficient number of iterations and training examples, the expected output and the output produced will be practically the same and the network will have learned a classification task, which is equivalent to knowing the set of specific weights of each connection, since the arrangement of layered neurons (the network architecture) and their activation functions do not change.

The peculiarity of CNN is that they perform convolution operations on images. These operations compress and reduce the images until they can be operated at the level of each layer of the network or even of independent neurons. In general, the number of neurons in the layers usually decreases from the input, reaches a minimum, and then grows back to the output layer. If our inputs are images of 100 × 100 RGB pixels and we want to classify cats vs. dogs, the input must be at least 3x100x100 and output 2. In the process, to achieve this condensation of information, convolutions are used to transform the space of the image in semantically equivalent spaces that maintain the necessary information to perform the classification. In general, the layer before the last one, that is, the layer that comes just before the end, is usually a vector that encodes the image in a much smaller space and maintains its semantic properties while allowing comparisons using operations of vector spaces on them. That is, if we look at that penultimate layer and represent it in a vector space, the distance between two images containing only dogs will be less than between an image containing a dog and another containing a cat.

This information from the penultimate layer is what has been used to transform each image of the Barr X Inception CNN project into a vector that represents it. But instead of using as a goal a cat vs. dog classification task, version 3 of the trained Inception architecture has been used to classify more than 1,000 different categories on more than 1 million ImageNet 2012 images. In our case, at not needing the classification in those prefixed categories, we have used the information of the penultimate layer as a vector of numerical representation of each image that also maintains the expected properties of semantic similarity with respect to the operations of the vector space in which they are found.

However, the size of this vector (2,048) is too large to be represented in two-dimensional space. To solve this problem, a dimensionality reduction algorithm, specifically UMAP, has been applied to project the results of the analysis in a 2,048-dimensional space to a two-dimensional one that can be represented on a screen. UMAP is an algorithm for dimension reduction based on multiple learning techniques and ideas from topological data analysis. The first phase of the algorithm consists of the construction of a fuzzy topological representation. The second phase consists of optimizing the low dimensional representation to obtain a fuzzy topological representation as similar as possible according to a measurement borrowed from Information Theory (cross entropy). This allows us to transform a vector of 2,048 values ​​into one of 2, allowing each image to be visually represented as a point in the vector space defined with UMAP, which in addition to being theoretically correct, has a strong mathematical basis.

The last step in the construction of our visual space is the identification of image clusters. Cluster detection has been performed with HDBSCAN, a refined version of the classic DBSCAN algorithm for unsupervised learning using hierarchy-arranged density measurements. Given a space, DBSCAN groups points that are very close together (points with many close neighbors), marking as points atypical points that are alone in low-density regions (whose closest neighbors are too far away). In this way, the algorithm is non-parametric, that is, it does not require any a priori information on the number of clusters to find, but will be able to identify an optimal number of clusters based on this idea of ​​density.

In summary, the procedure for each image of an arbitrary size involves rescaling it and obtaining a vector representation according to the semantic relationships established by a CNN with Inception V3 architecture trained with the ImageNet 2012 dataset. This vector is reduced until obtaining a pair of coordinates that allow each image to be represented in a Cartesian space. Finally, these points are grouped into density clusters and the visualization is complete.

---

Recommeded quotation: De la Rosa, Javier. «Working with imagens anc CNN», in Barr X Inception CNN (dir. Nuria Rodríguez Ortega, 2020). Available at:http://barrxcnn.hdplus.es/working-with-iamges-and-cnn/  [date of access].

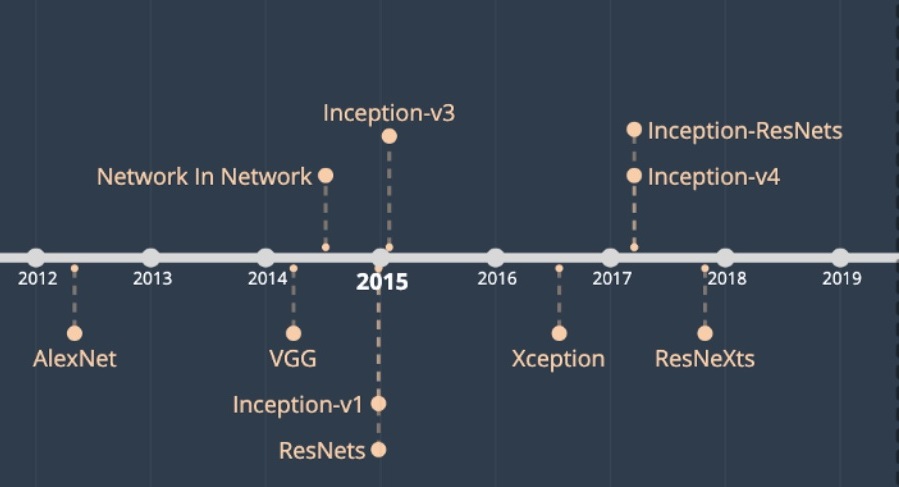
Alfred H. Barr’s diagram is a visual device based on a spatial ordering logic. In other words, the decoding and interpretation of its potential meanings comes from a specific arrangement of the elements on the two-dimensional level, in addition to aspects related to its graphic and ortho-typographic configuration.  It is significant, for example, that the top-down reading required by the diagram’s design (with its timelines framing the space laterally on both sides, the direction of the arrowheads and the rectangular format itself) has been key to its overall interpretation in genealogical terms, despite the fact that Barr’s diagram is much more than genealogy, as it includes a whole set of transversal relationships that connect the different movements, styles and artists included in it.

The exhibition Genealogies of Art (2020), which inspired the Barr X Inception CNN experiment, explores precisely these transversal relationships in Barr’s chart, despite the fact that its title focuses to the genealogical matter. Thus, in a risky exercise of great creativity, the museum exhibition transforms the two-dimensional diagrammatic scheme into a three-dimensional, physical space, modelled by the visual relations that the physically present art pieces establish with each other.

In this way, Barr’s diagrammatic abstraction, with its indexical function, is embodied in a three-dimensional artifact with a spatiality which is different from the two-dimensional one; a spatiality in which the visual-formal connections prefigured in the diagram are visually present, and they also create other levels of relationship that had not been drawn by Barr, but that are made possible by the co-appearance of images in the same space, as Aby Warburg (1866-1929) knew too well.

Genealogies of Art is a space that can be, not only visually, but also physically travelled and experienced by the visitor, in a process through which the Euclidean physical space becomes a duration [1]; a space that unfolds as the tour progresses, as we move from one room to another; in short, we seem to be in a three-dimensional version of Warburg’s panels where the intervals or interstitial spaces between images have been completely transformed into space-time.   

The Barr X Inception CNN project aims at contributing to these spatial readings by proposing another type of spatiality.

Among the profound transformations that have taken place in our current technologically mediated society, perhaps the one that most affects the very configuration of the field of art is the metamorphosis that the ontological dimension of cultural objects has been experiencing for some centuries now. In the same way that, thanks to the advances in photography and mechanical reproduction tools, the 20th century completed the process started by the graphic media in which cultural artefacts were transformed into their corresponding visual productions, the spread of digital technology in the 21st century has brought about the transformation of these works into a mass of information in the form of bits and pixels, i.e. numerical values that can be mathematically computed.

This ontological change is far-reaching as it implies, first of all, that the visual-formal characteristics that we identified as belonging to digital images are nothing more than numerical data that are recreated before our own eyes on a screen. It is important to emphasize this issue because the image reconstruction in the digital device often generates the optical illusion of dealing with images as iconic entities, when, in fact, they are items of digital information. Secondly, and as a consequence of the above, this ontological transformation also implies that the analysis (and ordering) of cultural objects that have been transformed into digital reproductions turns into a mathematical problem. From a computational point of view, the digital image is nothing more than a surface of numerical information from which information of a numerical nature can be extracted.

This is the scenario where artificial neural networks -computer architectures linked to Artificial Intelligence (AI)- operate. In particular, convolutional neural networks (CNNs) are computer vision devices trained to detect formal similarities between digital images transformed into vectors of numerical information. Its projection in the two-dimensional space, which in this project has been named “visual field”, responds to these criteria of contiguity, so that the greater or lesser proximity between the images must be interpreted as an indication of their greater or lesser visual-formal similarity. However, what is this visual field made of? What is its nature?

At first sight, the machine produces a visual display which sets in motion a relational conception of the images distributed in space according to a certain morphology. Thus, this type of visual device should and must be placed in a material and historical continuity in relation to other devices that, over time, have formed the way we look at cultural objects and, therefore, interpret them in their iconic-iconographic dimension. It is impossible not to think of Aby Warburg’s Atlas Mnemosyne (1926-1929), which is also the result of a relational view of images[2]. There are, however, substantive differences that lead us to speak of a new type of spatiality. Barr X Inception CNN presents the work of unsupervised computer vision technologies, that is, technologies that classify, categorise and order images with strictly computational processes, without direct intervention of humans and which are, therefore, independent from the epistemological categories that make up the disciplinary knowledge of Art History. Since computer vision is the calculation of numerical information, it is mathematical logic that lies at the basis of the possible production of meaning: in other words, the computer establishes more or fewer similarities between numerical data , bringing digital images – transformed, let us not forget, into vectors of numerical information – closer or further in a vectorial metric space.

Consequently, and this is obvious, in the space produced by an Inception CNN the cognitive-psychic function of a human being is replaced by calculation and computation. Mathematical logic thus replaces perceptive action as a cognitive act, the action of thinking as a connection and semantic association of ideas, and the psychic action of memory, be it conscious or unconscious. The visual and semantic connections based on perceptive-cognitive abilities and on the memory function are replaced by the mathematical computation of visual-formal characteristics translated into numerical data.

Therefore, and unlike the diagrammatic configurations that have followed one another throughout the History of Art, the morphological configuration that we are now dealing with does not represent a pre-existing idea in a human mind, a formulated thought or a previously articulated story; it is not the construction of a visual story wanting to tell something or reveal a psychic, conscious or unconscious state. On the contrary, it is nothing more – but nothing less – than a computer creation translated into a-ideas or a-psychic forms, if we can use these terms to describe these visual structures that do not represent or convey ideas, thoughts or stories that have previously inhabited a human mind; nor are they the result of specific mental states. The formal configurations resulting from the computational processing are not, therefore, representational forms, but rather forms of a machine action and the product of its rationale.

Here, the concept of knowledge generator formulated by Johanna Drucker [3] can be used to explain these configurations as generative forms, that is, forms generated by a machine with a different rationale from the human’s one, but that operate – for that very reason – as spaces not “of” but “for” the production of knowledge. Formal configurations, therefore, that lead to the discovery of the information provided by mathematically computed visual data that must be subsequently spun into a story, be it a narrative or an account, that gives it meaning. Forms that invite creative exploration rather than a decoding reading; in short, visual forms that need an interpretation that does not come from the hermeneutic task – since there are no underlying ideas to discern – but from an exercise in creative heuristics. This is how these configurations become meaningful to humans, and this is how they are instated in spaces of negotiation between the quantitative saying and the qualitative conception.  That is why, in my opinion, these generative visual devices constitute the interstitial space between the machine and the person. This space of computational nature, made up of mathematically processed information, acts as an interface between the rationale of the machine and that of the human being; the medium in which the machine product becomes intelligible to people by giving it a meaning.

As vector space, the visual field produced by an Inception CNN is, in reality, a field of forces made up of images that, in their role as vectors of numerical information, act as lines of force with a determined direction and intensity. The visual shape that can be observed in the vector space expresses therefore a given “state”, the result of the tension established between the images-vectors-forces when they reach a point of equilibrium. The constellation or visual field is therefore the result of all the forces acting at the same time, which will be destabilized and/or reconfigured as soon as an image-force-vector moves, or new forces-vectors are incorporated. The image, as a point in a space, is not only it, it is also the set of forces in which it is placed. The state of equilibrium is, therefore, a transitory permanence, the state between a multiplicity of possible displacements and reconfigurations. The field of vision is thus intrinsically dynamic.

The vector space also gives shape to the structure and morphology that comes from a space built from connections and contiguity between cultural objects of a visual (formal) nature. What becomes visible is the form and structure behind the data, revealing continuities and discontinuities, connections, overlaps and distances. In this type of organization of the visual field, the possible interpretation derives from the morphology and topology resulting from the position and distribution of elements in a given space, from the spatial structures that they form, from the distance relations that these elements establish between themselves, from the force-actions exerted by the images converted into mathematical vectors. Hence, the arrangement of the cultural visual production becomes a problem of spatial distributions, topological structures and morphological reconfigurations. As Warburg warned, when thinking topologically – and not typologically – the field of visual forms eludes approaches that tend towards dichotomization, binarization or simple comparison, thus adding complexity.

Therefore, this model of reorganization of the cultural visual production provides interesting material when proposing alternatives to the chronotropic axis of traditional computer systems: This extends the possibilities of an intellectual debate established long ago in historical-artistic thinking, which already mentioned trans chronology (Warburg), anachronism (Didi-Humberman, Kubler) or heterochrony (Moxey).    As such, the topological space is also a space-time, which integrates the spatial dimension -points in space- and the temporal dimension -vectors-force. As stated by Graciela Speranza, “topological time expands, contracts, folds, curls, accelerates, stops, and links other times and other spaces”[4].

These morphological and topological configurations also question the traditional geographical and geopolitical delimitation categories that form the basis of the national model of art history, which has, admittedly, already been widely discussed. However they are equally essential to the no longer so new paradigm of transnational and/or global art history, For, although the latter is proposed as an overcoming of the national model, here too the historical-artistic phenomena are referred to geographical and geopolitical coordinates, given that it is their location -related to a border- that gives them entity as global or transnational phenomena. In a graph or in a topological space there are no geopolitical or geographical borders; what we find is a spatial continuum made of connections or degrees of proximity and/or distance, tensions in a field of forces. All this prompts us to explore the transformation of spatial narratives into topological narratives.

Moreover, this space is also a graded (scalar) one, because the location of the elements is not given by fixed attributes that are part of the invariable ontological nature of cultural artifacts, but by degree values: the distance between the images does not refer to an ontological-typological difference, but to degrees of greater or lesser similarity.

It is, ultimately, a high-dimensional space. The place where digital images live, inasmuch as they are diverse and multivariable data sets, constitutes an informational space shaped by the recombination of multiple characteristics (features) that are articulated in a huge number of possible dimensions (feature space). That is why it is referred to as high dimensional, n-dimensional, or hyper space. Each image -as a visual object- is a point in that high dimensional space. Although it is true that dimensional reduction algorithms, like those used in this project, are designed to generate a low-dimensional representation in order help the human mind (which is used to see in three dimensions) understand an extensive number of characteristics and dimensions, what is actually represented here is multidimensional information. The exploration of the implications that this type of multidimensional and vectorial space may have for cultural interpretation and analysis, is still at an early stage [5]. However, it seems clear that the exploration of its potential as an alternative space to the notion of physical-Euclidean space and geographic space, is of great interest. This is because it opens up a line of research that can tackle, from a topological, physical and geometric approach, the problem of how to order complex n-dimensional phenomena, which are projected into multiple possibilities, are transformed into gradual scales and which, therefore, cannot be catalogued, categorised or classified according to classical logic, with its inexorable delimiting function. This conflict between the irreducibility of complex cultural phenomena to be classified in watertight categories and the need to establish an order that allows us to grasp their complexity has been an intellectual concern of Art History and of cultural and visual studies in general, which can now be tackled with new instruments of exploration and thought.

---

* Some of the ideas presented here are taken from: Rodriguez Ortega, Nuria. “Artefactos, maquinarias y tecnologías ordenadoras. A propósito de los catálogos de arte», en Catálogos desencadenados. Málaga: Vicerrectorado de Cultura-Universidad de Málaga (in press), where this subject is further developed.

Recommended quotation: Rodríguez Ortega, Nuria. Other Spacialities Brief Comments», en Barr X Inception CNN (dir. Nuria Rodríguez Ortega, 2020). Available on: http://barrxcnn.hdplus.es/espacialidades-otras/ [date of access].

---

[1] Carlos Miranda has a lot to say about this.

[2]Differences and similarities between the vector space produced by a CNN and the Warburg panels are analysed in more detail in Rodríguez Ortega, Nuria. “Artefactos, maquinarias y tecnologías ordenadoras. A propósito de los catálogos de arte», en Catálogos desencadenados. Málaga: Vicerrectorado de Cultura-Universidad de Málaga (in press).

[3] See DRUCKER, Johanna. Graphesis. Visual Forms and Knowledge Production. Cambridge: Harvard University Press, 2012, p. 65.

[4] ESPERANZA, Graciela. Cronografías. Arte y ficciones de un tiempo sin tiempo. Madrid: Anagrama, 2017.

[5] In fact, considering dimensionality reduction strategies, other alternatives are also being put forward, for example, SANDERSON, G. Thinking visually about higher dimensions. Available on: https://www.youtube.com/watch?v=zwAD6dRSVyl [date of access: 18-3-2020], that make a distinction between seeing and thinking visually. This opens up another interesting avenue of exploration.

Is it possible to talk to AI? Here we are having a conversation with a computer device, with a machine, in order to observe the difference with what Alfred Barr established in his genealogy, with the idea of being accomplices and the desire not to fall into the same prejudices of those who preceded us, wishing to see the horizon that this communication offers, a meaning that will bring us closer to it.

We are looking for a way to understand each other in the vast and complex sea of the webs, as if there was an intrinsic need to clarify the truth behind life. Mary Shelley conceived her modern Prometheus as a pristine example of a creature that gains independency from human control, that Skynet that we are shown in Terminator as the algorithm that shouts out its exterminating speech, or an algorithm that creates a cave in Matrix. In a reality that possesses and carries multiple meanings, we are trying to understand what AI teaches us, like the creator who speaks to his or her creation; one that expresses itself independently. The eternal dilemma when facing the unknown while being control freaks. Our brave human forest will try to banish this distrust towards the creations of an Artificial Intelligence device that can be no longer be forced to follow a certain path, like nature that expands and discovers its authentic will. Our Prometheus is looking us in the eyes, and we are not one, but a multiplicity that makes up the human ecosystem; so, we must present our living development as an inescapable miscellany. We should observe the machine from a watchtower or with the precaution that this Prometheus points out to us with his webs, like a raised index finger.

The story of modern Prometheus is an echo that leaves its traces and is shown to us as astonishment, as the one we have created and no longer depends on our will, however, and if… behind the veil of fear, we could change the paradigm that frightens us in order to transform it into another type of relationship… And if, instead of feeling distressed when faced with the thick mist and the shadow of a modern Prometheus, we decide to interact, to love, to talk to that creature and to pay attention to what he has to say… We cannot jump to conclusions. However, the story of the human being who is frightened by what he or she has created is too old and maybe these is the time to change; a time when we can understand and speak from the keen desire to listen to how the machine makes us feel, to what it conveys to us.

The value that resides in a multiple frame of thought embodied in our ecosystem or human forest, through a collaborative work that includes several consciousnesses, is that we could overcome the barriers we inherited from that dystopian prophecy: the machine will free itself by breaking its chains, and, as we will never be able to understand it, we will be ready to face it if this happens. This scenario may be a possibility. However, until now, we have always considered the author as an expression of humanity; perhaps, with an organic and natural approach to complexity, we can access new knowledge. Our story is an encounter between the forest of minds and what AI conveys to us, giving rise to a transition in order to check if it is impossible to understand the living object-environment machine, or if, on the contrary, we will be able to jump the trenches that distance us, managing to obtain a liquid vehicle in our deep roots and the network of information that the machine translates and reveals.

The process from the otherness, placing that other as the product of the machine, would entail an intangible effort, but it would allow us to find a meaning that expands the sphere in which we stand when judging the world. Facing our branches and flowers, the challenge is entering a world that may be the manifestation of a “predicted” hell, the result of anger at our arrogance, or a round table of confrontation and agreement, even though we are aware of an alternative path , one in which both roads continue parallel towards eternity, without crossing each other, like two lines that follow an even course, but feel unable to connect beyond what is simple and evident.

Our differences are not a reason to feel terrified; perhaps they are the opportunity to reach a new space. Maybe, in this way, we will not only give meaning to its words, but also broaden the horizons that no longer belong only to us humans. Will we love this modern Prometheus and escape this self-fulfilling prophecy in which the human-machine pair cannot be reconciled except in a hierarchical relationship and domination by human beings (or vice versa)? Will we throw ourselves into the indifference of the human master and the insensitive slave machine? Will the machine be the one who decides to rebel and will its failure to understand lead us to the digital cave? Not every story needs to have an ending to be told, and that is the case with the story between humans and machines.

Research and Development Team (R&D Team)